Easy question: What digit (0-9) is this?

It was a “2”. Got that? Well, this should also be another easy question: What digit is this?

If you said, “it’s not a digit, it is the letter Q” you are wrong. Listen to the rules again: What digit (0-9) is this? The answer is of course 8, as seen here by the output of a 3 layer MLP neural network:

Not convinced? Well you should be. With enough training samples and epochs the neural net has great accuracy of reading handwritten digits.
OK, what? Back to the beginning – what are we even talking about?
A foundational piece of machine learning, really one the early tasks that can’t simply be programmed away, was recognizing handwritten digits. This work goes back to the 1990s and the first (artificial) convolutional neural networks. It is basically impossible to program in if/then statements to identify a number 2. You could write code that says if pixel places 620-630 are all greater intensity than 0.8, then you probably have a line on the bottom, hence a feature of a number 2. But obviously that does not scale or work with all the variability of how people write.
Take this handwritten “3”. How do we know it is a 3? Well, come to think of it, actually I do not. This particular piece of data was not labeled by the author. Another problem for another time.
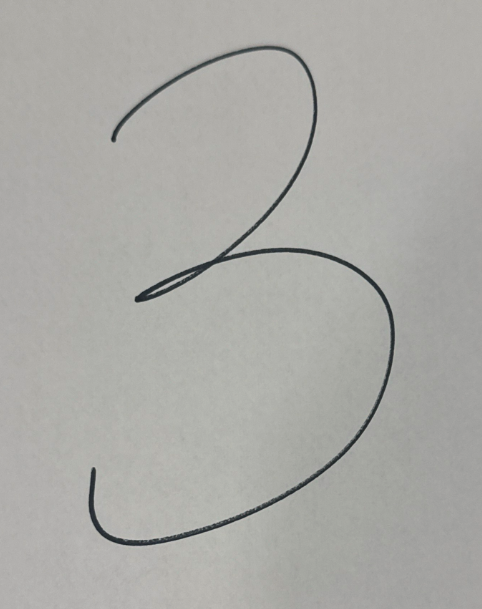
MNIST focused on taking handwritten digits and converting them to 28×28 grayscale so machines could process them. So first, convert this to a 28×28 grayscale:
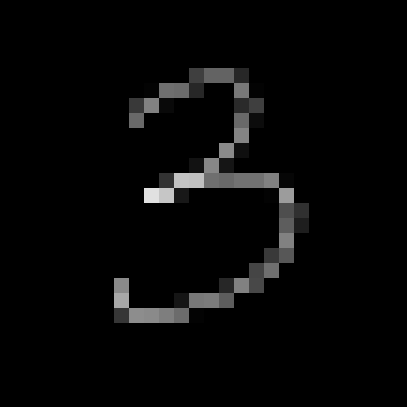
Now visualize that as a 28×28 matrix, each element between 0-255 (8-bit):
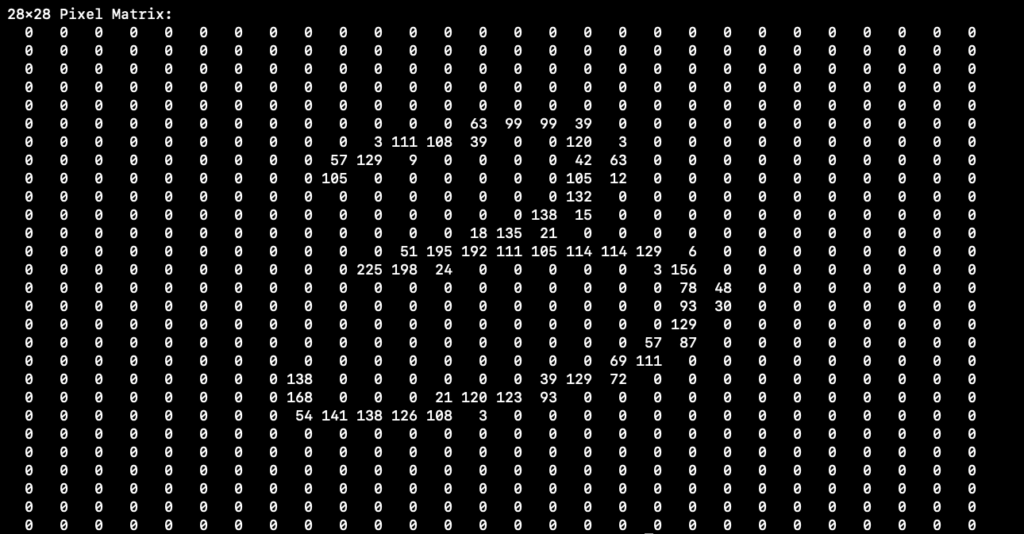
That is perfect for working with machines. Notice this can just be a 784 element column-vector with values 0-255 in each place. We build our neural network as follows:

784 neurons on the left, one for each pixel of the input. 10 neurons on the right, one for each output possibility (0-9). Sticking with our “3” that means input X151=63, X152=99,(those are the first nonzero pixel inputs you see in the matrix above) … straight to the end where pixel 784 or X784=0. The outputs should be [0 0 0 1 0 0 0 0 0 0] meaning we have 100% confidence the input is a “3” and not something else. Don’t worry about the AI black box magic right now, we’ll address that in a minute. Here is the actual output we get:
===============================================
SINGLE TEST SAMPLE SOFTMAX OUTPUT PROBABILITIES
===============================================
True label: n/a → Model predicted: 3
Confidence: 0.892576 (89.26%)
----------------------------------------------
Class Name Softmax Prob Bar
-----------------------------------------------
0 0 0.000000 ░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░ 0.00%
1 1 0.000001 ░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░ 0.00%
2 2 0.000001 ░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░ 0.00%
3 3 0.892576 ████████████████████████████████████████ 89.26%
4 4 0.000000 ░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░ 0.00%
5 5 0.091811 █████░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░ 9.18%
6 6 0.000000 ░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░ 0.00%
7 7 0.000000 ░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░ 0.00%
8 8 0.014620 ░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░ 1.46%
9 9 0.000992 ░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░ 0.10%
-----------------------------------------------
PREDICTED CLASS: 3 (3) with 89.26% confidence
===============================================
A well-communicated written “3” There is still a 10% chance it is a 5 or 8, but that’s just 2 times through (also known as 2 epochs) the training set of 60,000 MNIST digits. As we go to 10 epochs and beyond the output neurons do go to 100% (or [0 0 0 1 0 0 0 0 0 0] more specifically). Here is how the model (python script you can pull from GitHub, link at the bottom) is invoked
./mnist_digits_10.py --train_classes d --test_classes d --test_samples 1 --epochs 10 --show_softmax_output_probabilities --test_seed 24 --train_samples 60000
Training on classes: ['d']
Testing on classes: ['d']
Using device: mps
Proportional dataset created:
digit: 60000 samples (100.0%)
Loaded MNIST test dataset: 10000 samples
Using train_seed=42 for training data selection
Using test_seed=24 for test data selection
Using 60000 training samples and 1 test samples
Model created with 10 output classes
Starting training for 10 epochs
Epoch 1/10, Samples: 3200/60000, Loss: 1.2241
Epoch 1/10, Samples: 6400/60000, Loss: 0.473
...(skipping to the end of training output)...
Epoch 10/10, Samples: 51200/60000, Loss: .01
Epoch 10/10, Samples: 54400/60000, Loss: .01
Epoch 10/10, Samples: 57600/60000, Loss: .01
Training completed in 20.21 seconds
Average time per sample: 0.03 ms
==================================================
SINGLE TEST SAMPLE SOFTMAX OUTPUT PROBABILITIES
==================================================
True label: n/a → Model predicted: 3
Confidence: 1.000000 (100.00%)
--------------------------------------------------
Class Name Softmax Prob Bar
--------------------------------------------------
0 0 0.000000 ░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░ 0.00%
1 1 0.000000 ░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░ 0.00%
2 2 0.000000 ░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░ 0.00%
3 3 1.000000 ████████████████████████████████████████ 100.00%
4 4 0.000000 ░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░ 0.00%
5 5 0.000000 ░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░ 0.00%
6 6 0.000000 ░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░ 0.00%
7 7 0.000000 ░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░ 0.00%
8 8 0.000000 ░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░ 0.00%
9 9 0.000000 ░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░ 0.00%
--------------------------------------------------
PREDICTED CLASS: 3 (3) with 100.00% confidence
==================================================
What if we train less? like instead of 60,000 training images and 10 epochs, how about 100 training images and 2 epochs (so it will only be exposed to 20 “3”s, 10 “3”s 2 times each)
./mnist_digits_10.py --train_classes d --test_classes d --test_samples 1 --epochs 2 --show_softmax_output_probabilities --test_seed 24 --train_samples 100
Training on classes: ['d']
Testing on classes: ['d']
Using train_seed=42 for training data selection
Using test_seed=24 for test data selection
Using 100 training samples and 1 test samples
Model created with 10 output classes
Starting training for 2 epochs
Training completed in 0.19 seconds
Average time per epoch: 0.09 seconds
Average time per sample: 0.94 ms
=================================================
SINGLE TEST SAMPLE SOFTMAX OUTPUT PROBABILITIES
==================================================
True label: 3 → Model predicted: 0
Confidence: 0.137974 (13.80%)
--------------------------------------------------
Class Name Softmax Prob Bar
--------------------------------------------------
0 0 0.137974 ███████████████████████████████████████ 13.80%
1 1 0.074135 ███████████████░░░░░░░░░░░░░░░░░░░░░░░░ 7.41%
2 2 0.088325 █████████████████████░░░░░░░░░░░░░░░░░░ 8.83%
3 3 0.113393 ██████████████████████████████░░░░░░░░░ 11.34%
4 4 0.102612 ██████████████████████████░░░░░░░░░░░░░ 10.26%
5 5 0.104179 ██████████████████████████░░░░░░░░░░░░░ 10.42%
6 6 0.103599 ██████████████████████████░░░░░░░░░░░░░ 10.36%
7 7 0.080653 ██████████████████░░░░░░░░░░░░░░░░░░░░░ 8.07%
8 8 0.106269 ███████████████████████████░░░░░░░░░░░░ 10.63%
9 9 0.088862 █████████████████████░░░░░░░░░░░░░░░░░░ 8.89%
-------------------------------------------------
PREDICTED CLASS: 0 (0) with 13.80% confidence
=================================================
A lot worse. The model has not learned. And we have our first hallucination — we fed it a “3” and the AI said we have a “0”. That’s bad.
But what about our Q that the model said was an 8? From a hallucination standpoint, our fundamental limitation is that network only had 10 output neurons. No matter what it was fed, it had to output something between 0-9. Therefore, the “Q” became an “8”. Look at this: what digit is this?

You can see from the label on the top — truly this is a whitespace (ws). There is nothing there. Yet the MLP neural net predicted this was in fact a “5”. How close was it?
./mnist_digits_12.py --train_classes d --test_classes w --test_samples 1 --epochs 10 --show_softmax_output_probabilities --test_seed 327 --train_samples 10000 --visualize 5
True label: 11 → Model predicted: 5
Confidence: 0.228395 (22.84%)
--------------------------------------------------
Class Name Softmax Prob Bar
--------------------------------------------------
0 0 0.062223 ██████████░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░ 6.22%
1 1 0.137581 █████████████████████████░░░░░░░░░░░░░░░ 13.76%
2 2 0.086253 ██████████████░░░░░░░░░░░░░░░░░░░░░░░░░░ 8.63%
3 3 0.066895 ████████░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░ 6.69%
4 4 0.085063 █████████████░░░░░░░░░░░░░░░░░░░░░░░░░░░ 8.51%
5 5 0.228395 ████████████████████████████████████████ 22.84%
6 6 0.110055 ████████████████████░░░░░░░░░░░░░░░░░░░░ 11.01%
7 7 0.104153 █████████████████░░░░░░░░░░░░░░░░░░░░░░░ 10.42%
8 8 0.062765 ███████░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░ 6.28%
9 9 0.056616 ███████░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░ 5.66%
-------------------------------------------------
PREDICTED CLASS: 5 (5) with 22.84% confidence
==================================================
As you would expect, not any conviction on this prediction, even going through the data with 10 epochs. Of course this was not a fair fight — I trained the MLP only on digits and asked it to find me a digit in a perfectly blank space.
How do we avoid this? We add in new classes for training: whitespace and Not a Number (NaN). When we train that way our results avoid hallucinations from being fed testing data that was outside the scope of the training data. We invoke the script now with classes d,ws for both training and testing:
./mnist_digits_10.py --train_classes d,w --train_samples 50000 --test_classes d,w --test_samples 1000 --epochs 10
Training on classes: ['d', 'w']
Testing on classes: ['d', 'w']
Proportional dataset created:
digit: 45454 samples (90.9%)
whitespace: 4545 samples (9.1%)
Loaded MNIST test dataset: 10000 samples
Loaded whitespace test dataset: 24000 samples
Proportional dataset created:
digit: 909 samples (91.0%)
whitespace: 90 samples (9.0%)
Using train_seed=42 for training data selection
Using test_seed=42 for test data selection
Using 49999 training samples and 999 test samples
Model created with 12 output classes
Starting training for 10 epochs
Epoch 1/10, Samples: 3200/49999, Loss: 1.4390
Epoch 1/10, Samples: 6400/49999, Loss: 0.5672
Epoch 1/10, Samples: 9600/49999, Loss: 0.3649
...
Epoch 10/10, Samples: 44800/49999, Loss: 0.0100
Epoch 10/10, Samples: 48000/49999, Loss: 0.0185
Training completed in 17.04 seconds
Average time per sample: 0.03 ms
Overall accuracy on 999 test images: 97.90%
Total Type I errors: 0 / 999 (0.00%)
Total Type II errors: 21 / 999 (2.10%)
Detailed breakdown:
Class 0: 97.9% (94/96) correct, incorrect: 2
Class 1: 100.0% (102/102) correct, incorrect: none
Class 2: 98.9% (89/90) correct, incorrect: 1
Class 3: 97.1% (101/104) correct, incorrect: 3
Class 4: 98.1% (104/106) correct, incorrect: 2
Class 5: 98.6% (71/72) correct, incorrect: 1
Class 6: 98.6% (71/72) correct, incorrect: 1
Class 7: 98.7% (75/76) correct, incorrect: 1
Class 8: 93.3% (84/90) correct, incorrect: 6
Class 9: 96.0% (97/101) correct, incorrect: 4
Class ws: 100.0% (90/90) correct, incorrect: none
And beautifully we were fed 90 blank images and every time saw it as a blank. Perfect.
But look at the “8”s and “9”s – only 93.3% and 96% accurate there.
But this whole exercise got me thinking:
Is it possible to avoid hallucinations by training to avoid hallucinations?
Stated another way, “Is it possible to get better accuracy identifying 0-9 digits (using the same amount of computational power) if you train on digits *and* whitespace *and* non-numbers?”
Our end goal is to avoid a digit to digit hallucination. We don’t want to be presented with a 4 and say it is a 9. That is a Type II error, and what we want to avoid at all costs. Let’s look at standard training with just digits (using backslashes for readability):
./mnist_digits_10.py \
--train_classes d \
--train_samples 50000 \
--test_classes d \
--test_samples 1000 \
--epochs 10 \
--visualize 5 \
--test_seed 19
Total Type II errors: 19 / 1000 (1.90%)
Let’s look at one of the 19 failed OCR attempts, a 4 that was misread as a 9.
Class 4: 98.0% (96/98) correct, incorrect: 1 (9), 1 (7)Note this particular digit error is a very bad 4 (half of the MNIST digits were written by high schoolers). However, it is labeled data, so we know without a doubt it is truly a 4.

Note our total Type II errors are at 1.9% — now, if we give the exact same testing data (including this bad “4”) but train now on 45000 digits plus 5000 not-a-number, do we get better results for digit-to-digit hallucinations? What do we predict for this “4”?
./mnist_digits_10.py \
--train_classes d,nan \
--train_samples 50000 \
--test_classes d \
--test_samples 1000 \
--epochs 10 \
--visualize 5 \
--test_seed 19
Total Type I errors: 1 / 1000 (0.10%)
Total Type II errors: 19 / 1000 (1.90%)
Class 4: 100.0% (98/98) correct, incorrect: none
So no better, no worse. 1.9% to 1.9%. Although the percentage remains the same, the individual errors are different. For example, our lousy “4” is now predicted properly (2nd of these 5 below):

but other errors come up including a single Type I error where we were given a digit and predicted it was not a number.
Let’s try this with 40,000 labeled digits, 5,000 not-a-number, and 5,000 blanks. Here is fuller script output :
./mnist_digits_10.py \
--train_classes d,nan,w \
--train_samples 50000 \
--test_classes d \
--test_samples 1000 \
--epochs 10 \
--visualize 5 \
--test_seed 19
Training on classes: ['d', 'nan', 'w']
Testing on classes: ['d']
Reported testing statistics will exclude impossible inferences
Visualization options: ['5']
Using device: mps
EMNIST letters: 80000 total, 52301 after excluding C,L,N,O,Q,R,S,W,Z,c,l,n,o,q,r,s,w,z
Loaded EMNIST letters dataset: 52301 samples
Proportional dataset created:
digit: 41666 samples (83.3%)
letter: 4166 samples (8.3%)
whitespace: 4166 samples (8.3%)
Loaded MNIST test dataset: 10000 samples
Using train_seed=42 for training data selection
Using test_seed=19 for test data selection
Using 49998 training samples and 1000 test samples
Model created with 12 output classes
Starting training for 10 epochs
Epoch 1/10, Samples: 3200/49998, Loss: 1.4763
Epoch 1/10, Samples: 6400/49998, Loss: 0.6118
Epoch 1/10, Samples: 9600/49998, Loss: 0.4315
...
Overall accuracy on 1000 test images: 98.00%
Total Type I errors: 2 / 1000 (0.20%)
Total Type II errors: 20 / 1000 (2.00%)
So, no. Went from 1.9% error rate to 2.0%.
After much testing, in general, unfortunately no, you can not get better results against hallucinations by training for hallucinations. It seems non-intuitive, but all that training compute is essentially wasted. The testing digits are always 0-9 and although you have learned blank and NaN, you are never presented those during testing. This holds to large epochs and smaller batch sizes. On Average, you do 0.3% worse on accuracy when you train with whitespaces, 0.15% worse when you train with not-a-number, and 0.2% worse when you train with both whitespaces and not-a-number. Boo. 😞
If you do want to avoid type II errors at all costs, the better way is simply rejecting all inferences where the confidence is less than some high percentage, say 99.95%. That gets to 100% across the entire MNIST test set of 10,000 accuracy even with five epochs. It is surprising to me that it is not confidence of 90% at just 2 epochs, but there are some really badly written digits in there, for example:

Rejecting low-confidence inferences is much more effective at avoiding hallucinations vs training for the unexpected.
Thanks for reading! And please, play with the code yourself — I published the code on GitHub.
==================================================
Appendix: Oh — we never dove back into the hidden layers. Here is the full 3 layer neural network.
The point of learning is to change the weights in the 3 layers (fc1, fc2, fc3) to minimize the error. Pytorch randomly selects initial weights and biases (example: in the range of (-0.09,0.09) for fc1) and then adjusts weights with each batch of trained images. Here is what our feedforward multi-layer perceptron (MLP) neural network looks like:
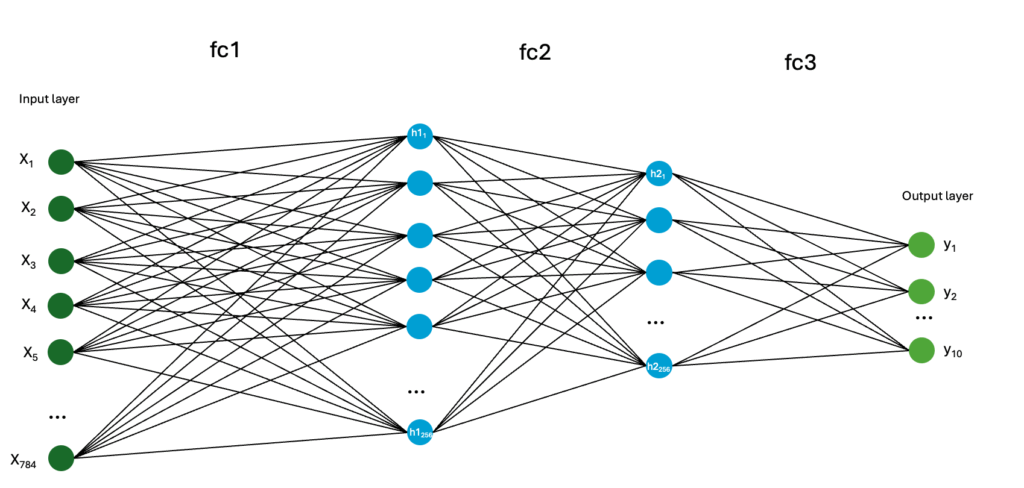
The input layer 784 long. Hidden layer 1 is 256 neurons. Hidden layer 2 is 128 neurons. Layer 3 is the output layer with 10 output neurons. Total of about 400 neurons. Fully connected, about 235,000 synapses.
If you were to count each input pixel input as neurons then their are 1,200 neurons. However, the input layer is just that and not neurons. Analogous to your eyes being rods and cones connected to neurons in the brain– the rods and cones themselves are not neurons. Also the input layer is not fed in as 0-255 (based on the greyscale intensity), it is fed in between 0-1 (that is raw intensity of that pixel value (input logit?) divided by 255).
Really, neurons are just matrix math. That first hidden neuron in blue (h11) is simply the sum of each weight times each input summed, plus it’s bias
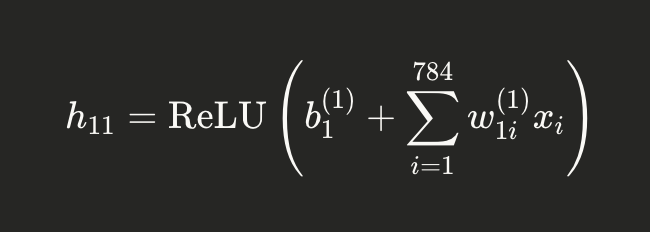
The ReLU just means that if the sum is positive, it stays. If the sum is negative, then h11=0. It stands for Rectified Linear Unit. Just doing this matrix math over and over again is what GPUs (and now we think maybe the human brain) does. Once it is learned, then the learned features (digits) are the AI black box magic inside the weights and biases.
