Ever wondered how odds map from a single game contest to a best of 7 series? For example, say you knew in any single game between team A and team B that team A will win 60% percent of the time. If they were to play a one game series on a neutral floor team A obviously advances 60% of the time. But what if they play a 7 games series (all on a neutral floor). What do team A’s odds improve to?
This can be computed analytically and straightforward. ChatGPT says to use the binomial distribution, but I’m not sure that’s 100% correct yet. Binomial will get you the probability team A gets exactly 5 wins in a 7 trials, but of course that can’t happen as after you win 4 the series is over. So, let’s just exhaust all possibilities between team H(favored) and team A(underdog):
For team H to win in 4 games there is one way: HHHH, total probability is p4 where p is defined as the probability team H wins any one game (60% from our original question). 0.64 = .1296 = 12.96% ≈13%. Meaning there is a 13% team H will sweep.
Team H can win in 5 games 4 different ways: HHHAH, HHAHH, HAHHH, AHHH. Each has a probability of p4 (1-p) = 0.05184 in our scenario. Multiplying by the 4 ways to achieve that result leaves a total probability of 4p4 (1-p) = 20.736%.
Team H can win in 6 games 10 different way and in 7 games 20 different ways (reader can check those for themselves), so final probability for team H to win a 7 game series is:
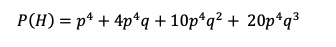
Where q is defined as (1-p)
Run the numbers and you find that 60% for a single game translates into 71% for a seven-game series (71.0208% to be exact). So, a 7 game series will draw out the better team by a benefit of 11% for a team that is already 10% better than a 50/50 coin flip.
Running the number for other values of p you get:
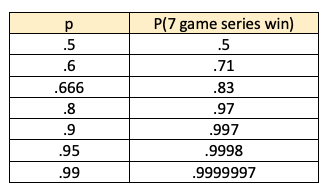
So it gives a 2x boost initially, with diminishing returns as you get past 80-90%. Charted out it looks like this:
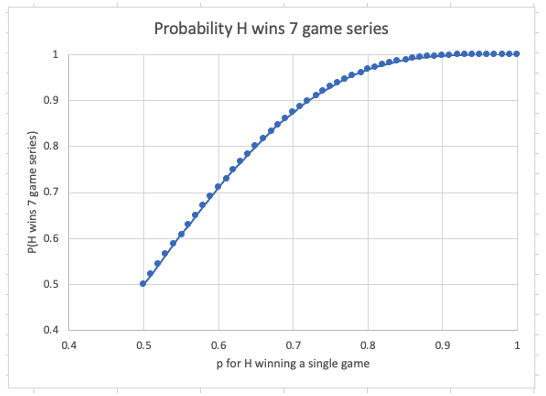
To me its compelling at p=80% or so. p=80% becomes 97%. p=80% means the team is -400 – bet $400 to receive $500. So—unless your team is a -400 favorite in game 1, don’t be too confident they will win the 7-game series. In fact, you can extrapolate the series winning odds from the odds from game 1.
Now, how about when team H wins the first 2 games? I’ve heard it said then for team A to win becomes impossible because they have to win 4 of 5 games. How likely is that? The formula there becomes:
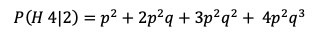
For a p=.5 that works to 81% Not very impossible at all, in fact will happen 1 our of 5 times.
Well, then why in the NBA when a team goes up 2-0 they win the series 95%? Because of course the team that goes up 2-0 is better than 50/50 against team B. More like p=0.66 – that gets you to 95% series wins after going up 2-0. Note, p=0.66 gets you only to 81% for the series before the start of game 1.
Summarizing the math:
If team A is 2x better (p(A)=.666, will win 2 times out of 3), then they win the series 81%.
If team A is 2x better (p(A)=.666, will win 2 times out of 3) and they win first 2, then they win the series 95%
If team A and team B are equal (50/50), then team A wins the series 50% (duh)
If team A and team B are equal (50/50) and team A wins the first 2, then team A wins the series 81%
If team A is worse (p(A)=.333) but wins first two games, they win the series 54% — even though they are worse.
Bottom line – winning a 7-game series after going down 0-2 is not hard – as long as you are the better team! Be twice as good and you have a 47% shot of pulling off the comeback.
